About

이번 포스트에서는 간단하게 회귀분석(Linear Regression) 의 개념과 Tensorflow 를 이용하여 학습하는 법에 대해서 알아보자.

목차

회귀분석(Regression Analysis)이란?

위키피디아의 정의에 의하면,

통계학에서, 선형 회귀(linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다.

여기서 독립 변수 는 입력값이나 원인을 나타내며, 종속 변수 는 결과물이나 효과를 나타낸다.

예) 집값을 예측하는 모델이라면 집값이 종속 변수(y)이고, 집의 위치, 방의 개수 등의 특징(Feature)들이 독립 변수(x)가 된다.

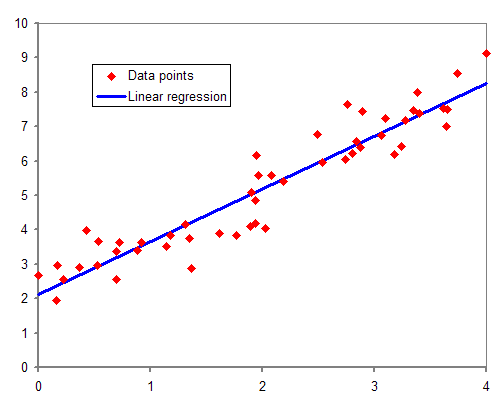
위 그림은 독립 변수 1개와 종속 변수 1개를 가진 회귀 분석의 예이며, 그 중에서도 선형 회귀(Linear Regression) 를 한 예이다.

여기서 선형 회귀 에 대해서만 간단하게 소개하자면 가장 널리 사용되는 기법이며, 종속 변수와 독립 변수의 관계가 선형(Linear) 인 경우에 사용한다.

회귀 분석 기법은 선형 회귀 외에도 다양한 종류가 있는데, 이 포스트에서 소개하지는 않을 예정이고, 나중에 링크의 내용을 번역하여 공유하도록 하겠다.(자세한 내용이 궁금한 사람은 위의 링크를 통해서 확인하자)

Tensorflow를 이용한 회귀 분석 실습

1. 데이터 전처리(Data preprocessing)

데이터 전처리는 이번 포스트의 주목적이 아니므로 자세한 설명을 더하진 않겠다.

# Import Dependencies
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.datasets import load_boston
boston = load_boston()

# 독립 변수와 종속 변수를 분리한다.
X_data = pd.DataFrame(boston.data, columns=boston.feature_names)
y_data = pd.DataFrame(boston.target, columns=["Target"])

# Train Test 데이터를 분리한다
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size=0.2, random_state=1)

# StandardScaler를 사용하여 스케일링한다
from sklearn.preprocessing import StandardScaler

# 객체로 사용해야 나중에 Test데이터에 같은 Mean, Variance를 사용할 수 있다.
scaler = StandardScaler()
scaler.fit(X_train)
X_train = pd.DataFrame(data=scaler.transform(X_train), columns=X_train.columns, index=X_train.index)
# 주의 : Test 데이터는 fit을하면 안된다! 객체 내부에 설정된 Mean, Variance값이 Update되기 때문에 여기서는 transform만 사용한다.
X_test = pd.DataFrame(data=scaler.transform(X_test), columns=X_test.columns, index=X_test.index)

# Tensorflow에서 사용할 땐 Numpy 데이터 타입으로 사용할 예정이니 변환하자
X_train = np.array(X_train)
y_train = np.array(y_train)
X_test = np.array(X_test)
y_test = np.array(y_test)
type(X_train), type(y_train), type(X_test), type(y_test)

이 예제에서는 Scaler로 StandardScaler(평균은 0으로, 표준편차는 1로 만드는 Scaler) 를 사용하였지만, 데이터마다 적절한 Scaler는 다를 수 있음을 명심하자. 역시 이 포스트에서는 자세히 다루지 않겠으며, 관심이 있는 사람들은 아래에 링크를 통해서 간략하게 이해를 하는 것을 추천한다.

2. Tensorflow Modeling

# Learning Rate
lr = 0.01

# 가중치를 몇번 업데이트 할 것인가?
epochs = 2000

# Features 독립 변수
X = tf.placeholder(dtype=tf.float32, shape=[None, X_train.shape[1]])
# Labels 종속 변수
y = tf.placeholder(dtype=tf.float32, shape=[None, 1])

# Weight 가중치, 초기값은 정규분포에서 랜덤하게 뽑는다
W = tf.Variable(tf.random_normal([X_train.shape[1], 1]))
# Bias 초기값은 정규분포에서 랜덤하게 뽑는다
b = tf.Variable(tf.random_normal([1]))

여기서 placeholder() , Variable() 메서드 사용법에 대해서는 이전 포스트를 참고하자. 

# tf.Variable을 사용했거나, 메서드 내부적으로 변수가 존재하는 경우에는 Variables
# 초기화해줘야 한다.
init = tf.global_variables_initializer()

# 우리가 예측하는 값 W*X + b
hypothesis = tf.add(tf.matmul(X, W), b)

# cost function으로는 MSE를 사용
cost = tf.reduce_mean(tf.square(y - hypothesis))

# Gradient Descent 방법으로 최적화
optimizer = tf.train.GradientDescentOptimizer(learning_rate=lr).minimize(cost)

# cost_history를 기록하면 마지막에 epoch 변화에 따른 cost 변화를 확인할 때 편리하다
cost_history = np.empty(shape=[1], dtype=float)

이렇게 필요한 Graph는 다 만들었으니, 이제 Session을 열어서 W, b를 update하며 Cost Function의 값을 최소화하는 작업을 실행하자.

with tf.Session() as sess:
    sess.run(init)

    for epoch in range(0, epochs):
        # optimizer에서 반환하는 값은 의미가 없으니 _로 받아주자
        _, err = sess.run([optimizer, cost], feed_dict={X: X_train, y: y_train})

        cost_history = np.append(cost_history, err)

        # 100 번에 한번씩 Error 변화를 확인하자
        if epoch%100 == 0:
            print('Epoch: {0}, Error: {1}'.format(epoch, err))

    print('Epoch: {0}, Error: {1}'.format(epoch + 1, err))

    # 우리가 설정한 Epochs만큼의 학습이 끝난 후에 나온 값을 확인하기 위해 받아두자
    updated_W = sess.run(W)
    updated_b = sess.run(b)

    # Test 데이터를 예측한 값
    y_pred = sess.run(hypothesis, feed_dict={X: X_test})

    # Mean Squared Error
    mse = sess.run(tf.reduce_mean(tf.square(y_pred - y_test)))

위의 코드들을 통해서 Tensorflow Session 을 이용하여 회귀 분석(Regression Analysis) 방법을 알아보았고, 아래에 Jupyter notebook 에서는 Tensorflow 이 제공하는 Estimator API 를 사용하여 Linear Regression 하는 방법도 추가되어 있으니 도움이 되길 바란다.

Jupyter Notebook

이 다음 포스트에서는 Tensorflow 로 인공 신경망(Neural Network) 을 구현하는 법에 대해서 작성하겠다.